This entry is an appendix for the previous entry: Data Experiment #04 Recover the sine curve.

I have compared a feed-forward neural network with a few other algorithms. As we see in the previous entry, the linear regression model achieves almost perfect accuracy. (No joke. If you have not read the previous entry, I strongly recommend reading it!) Therefore we do not use it for this comparison.

Results

The source code comparison.py for the comparison is available on Bitbucket. Here is the list of the roots of mean square errors:

• Decision Tree: 0.727957801196
• Support Vector Machine: 0.676060954329
• Random Forest: 0.481364276216
• Feed-forward Neural Network : 0.0878632475422

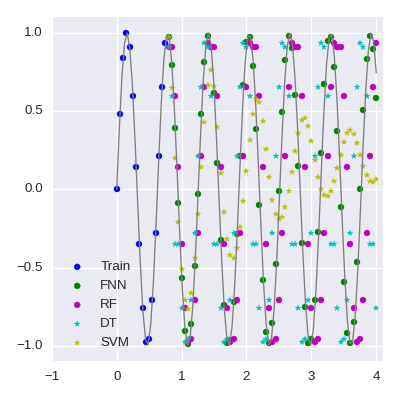
Comparison in details

I should mention at first that the decision tree, random forest and a feed-forward neural network use random numbers. In the source code I give random_state for reproducibility, but I did not it for the neural network, because it is not clear to do it. So the RMSE of the neural network model will change. But its RMSE is at most 0.2, namely the neural networks always gives the best score.

The tuning parameters for the models (except the neural network) are chosen by 5-fold cross-validation scores. The support vector machine uses the sigmoid kernel. This could be reasonable, but the result is very bad. (If we look at only RMSE, then the decision tree seems worse than the support vector machine, but if we also look at the scatter plot, the decision tree must be better than support vector machine at least for larger x.)

I follow the blog entry "Neural Nets: Time Series Prediction" for the structure of the neural networks. (But I did not read the code in details, so the structure which I create could be different from one in the lined page. At least our neural network model contains bias units.) The feed-forward neural network consists of two hidden layers which have 5 and 3 hidden units, respectively. All hidden and output units are tanh units.

I use Keras (with Theano backend) to create a neural network model. It is trained with 50000 epoch, but the training finishes in a short time.

The excerpt of the code for a neural network is following. A data frame df, ndarray X and the function ext_sine making a prediction are defined at a very first part of the code.

from keras.models import Sequential
from keras.layers import Dense

y = df[['y']].as_matrix() # target variable (nx1 matrix)
model = Sequential()
model.add(Dense(input_dim=3,output_dim=5,init='uniform',activation='tanh'))
model.add(Dense(input_dim=5,output_dim=3,init='uniform',activation='tanh'))
model.add(Dense(input_dim=3,output_dim=1,init='uniform',activation='tanh'))

model.compile(loss='mean_squared_error',optimizer='rmsprop')
model.fit(X,y,nb_epoch=50000,verbose=0)
result['FNN'] = [y[0] for y in ext_sine(model,'FNN')] # ext_sine() is a user defined function.