I found recently a very interesting blog entry "Neural Nets: Time Series Prediction". The entry is a demonstration of a neural network and the sample code is written in Scala. Because the author does not compare the neural network with other statistical learning algorithms, so I decided to do it. But ...

Problem: recover the sine curve from a small part of it

The values of $\sin(10x)$ are given for $x=0,0.05,0.10,\cdots,0.75$. Predict the values of $\sin(10x)$ for $x=0.80, 0.85,0.90,\cdots$.

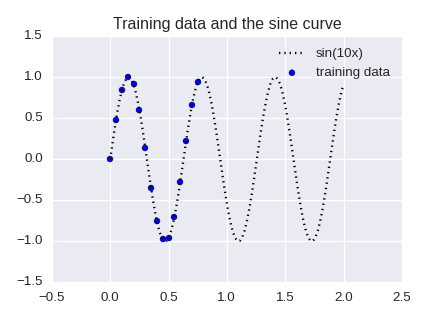
The idea is simple: detect a recurrence relation $f$ $$\sin(10(x+3a)) = f( \sin(10(x+2a)), \sin(10(x+a)), \sin(10x) )$$ by using a statistical learning. Here $a=0.05$. Therefore our training data look like the following table.

    x-coord            x0        x1        x2         y
0      0.15 -2.775558e-16  0.479426  0.841471  0.997495
1      0.20  4.794255e-01  0.841471  0.997495  0.909297
2      0.25  8.414710e-01  0.997495  0.909297  0.598472
3      0.30  9.974950e-01  0.909297  0.598472  0.141120
4      0.35  9.092974e-01  0.598472  0.141120 -0.350783
5      0.40  5.984721e-01  0.141120 -0.350783 -0.756802
6      0.45  1.411200e-01 -0.350783 -0.756802 -0.977530
7      0.50 -3.507832e-01 -0.756802 -0.977530 -0.958924
8      0.55 -7.568025e-01 -0.977530 -0.958924 -0.705540
9      0.60 -9.775301e-01 -0.958924 -0.705540 -0.279415
10     0.65 -9.589243e-01 -0.705540 -0.279415  0.215120
11     0.70 -7.055403e-01 -0.279415  0.215120  0.656987
12     0.75 -2.794155e-01  0.215120  0.656987  0.938000

If we denote by $x$ a value of the x-coord column, x0, x1, x2 and y are $\sin(10(x-3a))$, $\sin(10(x-2a))$, $\sin(10(x-a))$ and $\sin(10x)$ respectively.

import numpy as np
import pandas as pd

''' Prepare the training set '''
step = 0.05
df = pd.DataFrame(np.arange(0.15,0.80,step=0.05), columns=['x-coord'])
df['x0'] = np.sin(10*(df['x-coord']-3*step)) ## sin(x-3*step)
df['x1'] = np.sin(10*(df['x-coord']-2*step)) ## sin(x-2*step)
df['x2'] = np.sin(10*(df['x-coord']-1*step)) ## sin(x-1*step)
df['y']  = np.sin(10*df['x-coord'])          ## sin(x) <- target variable
print(df)

We have a very simple training data, so let's make a predictive model. The following image shows the rediction of a certain model which I trained. The prediction is perfect. (The RMSE is 4.61466567015e-15.)

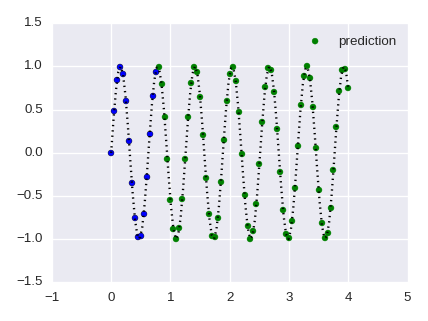
This model is not a neural network

Which statistical learning algorithm did I use? The answer is in the following code.

''' Create a linear regression estimator '''
from sklearn.linear_model import LinearRegression
fit_lr = LinearRegression()
fit_lr.fit(df[['x0','x1','x2']],df['y'])
print('coefficients:', fit_lr.coef_)      ## [-0.69092766  0.21269213  1.06423747]
print('intercept   :', fit_lr.intercept_) ## 8.32667268469e-17

Yes, this is just a linear regression. No trick. The estimated intercept is almost 0. Therefore we have a very simple recurrence relation:

$$ -0.691 \sin(10x) + 0.213 \sin(10(x+a)) + 1.064 \sin(10(x+2a)) = \sin(10(x+3a))$$

''' Make a prediction '''
yhat = []
x_test = np.arange(0.8,4.05,step=0.05)
X = df.ix[df.shape[0]-1,['x1','x2','y']].as_matrix().reshape((1,3)) ## initial input
for i in range(len(x_test)):
    pred = fit_lr.predict(X)[0] ## predict the value of sin(10x)
    yhat.append(pred)
    X = np.array([[X[0,1],X[0,2],pred]]) ## next input 
print('RMSE        :', np.sqrt(np.mean((np.sin(10*x_test)-yhat)**2)))

What is happening?

The initial guess could be to make use of $10a=0.5 \sim \pi/6 = 0.52...$. But this approximation is too rough to see the above accurate prediction. In fact we have a rigorous linear recurrence relation.

Remark. In the following discussion we observe $\sin(x+\alpha)$ instead of $\sin(10x+10a)$.

The key observation is the Fourier series expansion of $\sin(x+\alpha)$: $$\sin(x+\alpha) = \frac{e^{i(x+\alpha)}+e^{-i(x+\alpha)}}{2i} = -\frac{e^{-i\alpha}}{2i} e^{-ix}+\frac{e^{i\alpha}}{2i}e^{ix}.$$ Here $i=\sqrt{-1}$. Therefore $\sin(x)$, $\sin(x+\alpha)$, $\sin(x+2\alpha)$, $\sin(x+3\alpha)$ lie all in the complex 2-dimentional vector space spanned by $e^{-ix}$ and $e^{ix}$. (Replace $\alpha$ with $0, 2\alpha, 3\alpha$ in the above formula.) Thus they are linearly dependent (with complex coefficients).

(If you are not familiar with a Fourier series, you may replace two functions $e^{-ix}$ and $e^{ix}$ with two linearly independent vectors $\vec{a}$ and $\vec{b}$. Then you can understand the discussion surprisingly rigorously.)

Put $\sin(x+3\alpha) = \beta_0 \sin(x) + \beta_1\sin(x+\alpha) + \beta_2\sin(x+2\alpha)$ ($\beta_0, \beta_1, \beta_2 \in \mathbb C$). Looking at the coefficients of $e^{-ix}$ and $e^{ix}$, we can easily obtain the following formulas.

$$ \beta_0 = t, \quad \beta_1 = -2t\cos\alpha -1, \quad \beta_2 = t + 2\cos\alpha \quad (t \in \mathbb C).$$

Therefore we have the following formula

$$\sin(x+3\alpha) = t \sin(x) - (2t\cos\alpha +1)\sin(x+\alpha) + (t+2\cos\alpha) \sin(x+2\alpha)$$

which holds for any $t$. (You can directly check that the above formula holds.)

Our training data is enough to find a value of $t$ and the formula explains why the intercept is almost 0. I should also mention that we do not use a specific value of $\alpha$, namely the above formula also holds for any $\alpha$.

Other algorithms?

The linear regression gives an almost perfect analytical approximation, therefore I do not try other algorithms.

Edit [22.03.2016]: I compared a neural network with other algorithms. See the next entry.