Letzte Woche habe Ich an einem Programmierung Wettbewerb "Real Data - April 2016" teilgenommen. Der Wettbewerb besteht aus sechs Aufgeben, die mit maschinellem Lernen verbunden sind.

Vor dem Wettbewerb hatte ich vor, alle Aufgaben mit R zu lösen, aber fast alle Aufgaben sind für NLP oder Bilderkennung. Deshalb habe ich R nur für die erste Aufgaben verwendet.

1) Forecasting passenger traffic

Kürzlich habe ich eine ähnliche Aufgabe gemacht. Es geht nämlich um die Zeitreihenanalyse. Diesmal hatte ich die folgenden Trainingdaten:

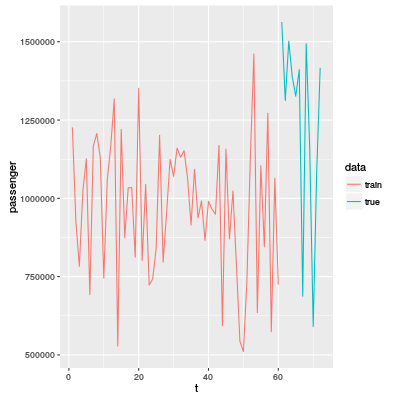
In der Grafik ist true die Daten, die man vorhersagen muss. Letzte Mal habe ich die Fourier-Transformation für eine Zeitreihe verwendet, aber diesmal nicht. Das liegt daran, dass die Periodizität nicht unklar ist.

Weil die x-Achse t des Kurvendiagramms ein Monat zeigt, deswegen kann man einfach eine Periodizität vermuten, aber wie das folgende Diagramm zeigt, ist sie nicht klar:

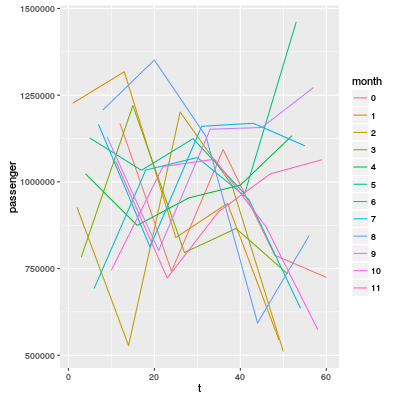
Obwohl die Periodizität unklar ist, habe ich je nach Monat lineare Regression-Modell gemacht. Die Note war nicht gut: 9.16/25. Weil die höchste Noten 14.81 war, war meine Note nicht schlecht.

Nun darf man die Quelltexte anderer Teilnehmer lesen, deswegen habe ich einige Quelltexte gelesen, mit denen man höher Note bekommen kann. Aber viele Quelltexte enthalten einige Parameter und es ist überhaupt unklar, woher die Parameter kommen.

Der Quelltext des Teilnehmers auf Platz 1 ist interessant, obwohl die Vorhersage nicht reproduzierbar ist. Die Idee ist sehr einfach. Er machte konkret eine Zufallsvariable, die die Anzahl von Fahrgästen entspricht und produzierte 12 Zufallswerte. Er ignorierte nämlich die Periodizität von der Anzahl. Ein konkreter Quelltext (auf R) folgt:

## yTrain ist der Vektor der Anzahl der Fahrgäeste
binWidth <- (max(yTrain)-min(yTrain))/10 ## bin=10
histInfo <- hist(yTrain,density=T,breaks=seq(min(yTrain),max(yTrain),by=binWidth))
x <- cumsum(histInfo$density)*binWidth
y <- histInfo$breaks[2:11]
quant <- approxfun(x,y) ## Lineare Interpolation
quant(runif(12,min=min(x),max=max(x))) ## Vorhersage

Die folgende Grafik ist der Vergleich von mehreren Methoden:

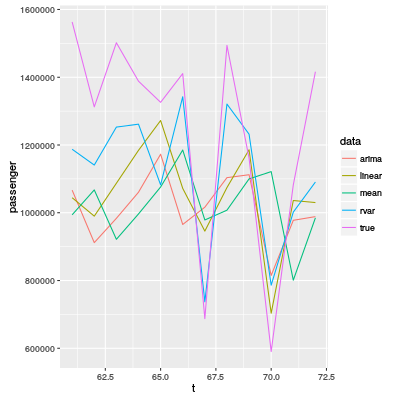
• true ist die Validierung-Daten.
• arima ist vom Teilnehmer auf Platz 19 (dieser Aufgabe) benutzt. Die Noten war 10.33 und der absolute Validierung-Fehler ist 3.196157.
• linear ist mein Vorhersagemodell. Der absolute Validierung-Fehler ist 2.70967.
• mean ist der Durchschnitt jedes Monates. Der absolute Validierung-Fehler ist 3.821018.

• rvar ist die beste Vorhersage, die der Quelltext produziert. Ich habe 10^4 mal das Modell versucht und der Quantil war

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  1.746   3.448   3.827   3.836   4.219   5.914
  

  Wenn man nur diese Resultat sieht, findet man nie das Modell gut. Falls man aber Glück hat, bekommt man natürlich sehr gute Vorhersage.

2) Language Detection

Die Aufgebe ist sehr einfach. Es gibt Texte auf verschiedene Sprachen: Deutsch, Englisch, Französisch und Spanisch. Die Aufgabe ist die Feststellung der Sprache eines Texts.

Stoppwörter sind die Wörter, die oft benutzt werden. Es ist genug, die Stoppwörter je nach Sprache in einem Text zu zählen. Was man beachten muss, ist nur die Umsetzung (encoding).