Ich habe kürzlich am Wettbewerb "Intro to Statistics" teilgenommen. Der wochenlange Wettbewerb besteht aus 22 Probleme und man schreibt normalerweise Quellentexte, um die Probleme zu lösen.
Um meine Kenntnisse auf Programmierung (vor allem Python) zu verbessern, löse ich Probleme auf HackerRank. Als ich den Wettbewerb gefunden habe, war er sehr interessant, deshalb habe ich mich dafür entschieden, an ihm teilzunehmen. Aber viele Aufgaben sind für Wahrscheinlichkeitstheorie statt Statistik, deswegen der Wettbewerb ist ein bisschen anderes als ich erwartete.
Während die Probleme meistens sehr einfach für mich sind, sind die letzte zwei Probleme sehr interessant. Die sind nämlich Vorhersagemodelle. Das eine ist für die Zeitreiheanalyse und das andere ist für Ergänzung der fehlenden Werte. In diesem Eintrag würde ich meine Erfahrung in der Zeitreiheanalyse etwas ausführlich erzählen.
Die Aufgabe
Die folgende Grafik zeigt die Anzahl der Personen, die eine bestimmte Webseite besuchten. Die Aufgabe war die Vorhersage der Anzahl in nächsten 30 Tagen.
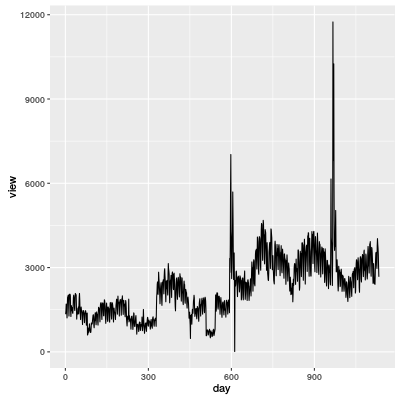
Aber man durfte beim Wettbewerb die Training-Daten nicht sehen. Deshalb ist es theoretisch nicht möglich, eine Vorhersagemodell nur für diese Daten zu machen. (Weil man schnell die Noten seines Modells bekommt, kann man mit den Noten sein Modell verbessern.)
Meine Strategie
Unter der Seite des Problems werden mehrere Ideen von einer Lösung gegeben. (Aber man muss eine der gegebene Methode nicht benutzen.)
Ich habe die Fourier-Transformation benutzt, um die Anzahl vorherzusagen. Aber je nach Wochentag habe ich ein Vorhersagemodell mit der Fourier-Transformation gemacht. Das liegt daran, dass die Graphen einfach werden. Das folgende Diagramm ist die Kurvendiagramme der Anzahl je nach Wochentag. Darin bedeutet "0" der originale Graph und 1–7 sind Wochentage.
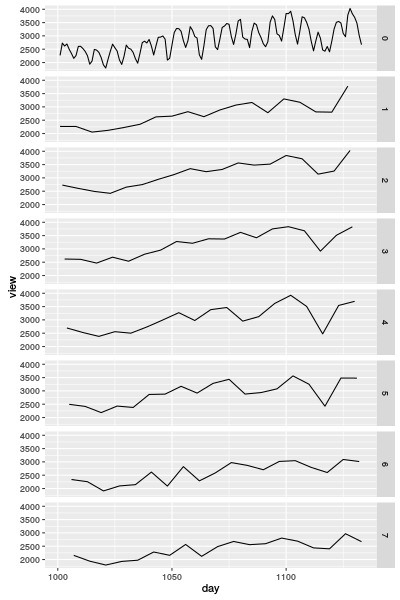
Vergleichung
Nach dem Wettbewerb kann man Quellentexte anderer Teilnehmer lesen. Während es ein Paar Betrüger gibt, habe ich einige interessante Quellentexte gelesen. Deswegen habe ich diese Vorhersagemodelle gemacht. Das folgende Diagramm ist das Ergebnis.
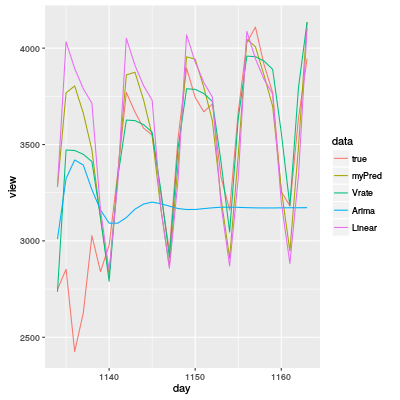
Ich habe auch noch mehrere Vorhersagemodelle mit Neuronalem Netz, Random Forest oder SVM, aber sie stehen nicht auf der Grafik, weil ihre Vorhersagen nicht gut sind.
myPred: Mein Vorhersagemodell (Fourier-Transformation je nach Wochentag). Der MAE (Mittelwert absoluter Fehler) ist 245.8667.Vrate: Ein interessante sehr gute Vorhersagemodell mit Veränderungsraten. Ein Quellentext davon in R ist am Ende dieses Eintrags. (Die originale Quellentexte sind in C++ oder Python geschrieben. Der MAE ist 173.1852.Arima: ARIMA ist ein der bekannten Modelle für Zeitreihen. Diesmal habe ich die automatische Optimierung (forecast::auto.arima()) für das Modell verwendet, aber die Vorhersage ist sehr schlecht. Also die "normale" Optimierung ist nicht genug für die Daten. Der MAE ist 448.5995.Linear: Eine einfache lineare Regression. Die einzige Kovariable ist der Tag ($>$1000). Obwohl das Modell sehr einfach ist, ist die Vorhersage relativ gut. Der MAE ist 309.4849.
Der Quellentext von "Vrate" in R
Ehrlich gesagt, der Quellentext ist auch verdächtig, weil drei Teilnehmer fast gleiche Quellentexte vorgelegt haben, obwohl die Texte richtig viel Konstanten enthält. Aber das Vorhersagemodell ist simple, deswegen habe ich das Modell in R geschrieben.
df ist der data frame, der die Daten der Zeitreihe erhält. df$view ist die Zielvariable. Die Idee ist einfach: Veränderungsrate der Anzahl je nach Wochentag mit kleiner Veränderung zu verwenden. Ich interessiere mich für die folgenden zwei Punkte.
- Große Veränderungen (≥40%) ignorieren.
- Die Mittelwerte der Veränderungen manipulieren. (1.0, 0.6, 0.6, etc.)
Die Hauptidee ist meiner Meinung nach, einen großen Fehler zu vermeiden. Es gibt mehrere "outliers" und mit der ersten Idee kann man erfolgreich die outliers vermeiden. Mit der zweiten Idee unterschätzt man die Veränderung, sodass die Vorhersagemodell keine große Veränderungen machte.
weekday.change <- rep(0,7)
weekday.count <- rep(0,7)
for (day in 2:N) {
change <- 100*(df$view[day]-df$view[day-1])/df$view[day-1] # Veränderungsrate
if (abs(change) < 40) { # Warum ist 40 die Grenze?
wday <- day%%7+1
weekday.change[wday] <- weekday.change[wday] + change
weekday.count[wday] <- weekday.count[wday] + 1
}
}
### Mittelwerte von den Veränderungen nehmen
weekday.change <- weekday.change/weekday.count
### weights geben
weekday.change <- weekday.change * c(1,0.6,0.6,0.6,0.3,0.6,1) # Woher kommen diese?
### mit Veränderungsrate vorhersagen
for (day in daysForPred) {
wday <- day%%7+1
x[day] <- x[day-1]*(100+weekday.change[wday])/100
}
### mysteriöse Veränderung
x[N+1] <- x[N+1] - 450

