Im letzten Eintrag habe ich die Aufgabe "Titanic: Machine Learning from Disaster" erklärt. In diesem Eintrag erzähle ich mein Ergebnis. Den Quellcode (außerhalb Forum) zu veröffentlichten, ist verboten, aber ich habe diesmal mit Python Datenanalyse gemacht.
Das Ziel ist ein besseres Ergebnis als das Geschlechte-Klasse-Preis-Modell (GKP-Modell). Ich habe das Ziel erreicht, aber ich bin nicht so mit meinem Ergebnis zufrieden.
Strategie
Man sollte die Test-Daten nicht sehen, wenn man ein Vorhersagemodell erstellt. Sonst wirken die Test-Daten das erstellte Vorhersagemodell und man wahrscheinlich das Modell nicht verallgemeinern kann. Aber das Ziel ist die Genauigkeit für die Test-Daten. Ich habe für die folgenden Gründe die Test-Daten gesehen.
- Die Anzahl der Leute, die zu einer bestimmten Gruppe gehört. Die brauche ich, um die Genauigkeit von meinem Modell für die Test-Daten zu schätzen.
- Die Daten mit Altern. Viele Alter fehlen in die Training-Daten und die Test-Daten. Aber die Alter sind wichtige Information, wie ich später erkläre. Deshalb habe ich ein Vorhersagemodell für Alter gemacht, um die fehlenden Alter zu ergänzen.
Die folgende Tabelle zeigt die Anzahl und die Genauigkeit von Ãœberleben für jede Gruppe von ("Sex", "Pclass").
| Sex | Pclass | Survived | CountInTrain | CountInTest | NaiveCount |
| female | 1 | 0.968085 | 94 | 50 | 48 |
| female | 2 | 0.921053 | 76 | 30 | 27 |
| female | 3 | 0.500000 | 144 | 72 | 36 |
| male | 1 | 0.368852 | 122 | 57 | 35 |
| male | 2 | 0.157407 | 108 | 63 | 53 |
| male | 3 | 0.135447 | 347 | 146 | 126 |
Mit der Tabelle kann man sofort ein einfaches Modell erstellen: Man hat überlebt, wenn die Wahrscheinlichkeit der Gruppe, zu der man gehört, ist gleich oder großer als 0.5. (Das Modell ist äquivalent zu dem Geschlechtes-Modell.) Das GKP-Modell benutzt den Preis (für Frauen mit Pclass=3), um das einfache Modell zu verbessern.
Die Genauigkeit der Gruppen von Frauen mit Pclass=1 und 2 sind schon hoch. Deshalb wollte ich die Genauigkeiten der anderen Gruppe verbessern.
Vorbereitung von den Daten
Erstens habe ich die Daten mit Alter von den Training- und Test-Daten genommen, um ein Vorhersagemodell für Alter erstellt. Ich habe SVM für den Algorithmus benutzen. (Der Mittelwert von RMSE für CV-Mengen ist 14.381.) Mit dem Vorhersagemodell habe ich alle fehlenden Alter ergänzt.
Zweitens habe ich die Spalte "Name", "Ticket" und "Embarked" gelöscht. "Name" und "Ticket" verursachen overfitting. Dass "Embarked" nicht relevant für Ãœberleben ist, denke ich, obwohl ich die Spalte benutzt habe, um die Alter zu schätzen.
Dritten habe ich die Spalte "FamilySize" gemacht. Sie ist die Summe von "SibSp" und "Parch".
Schließlich mache ich die Spalte "inCabin" gemacht. Sie ist 1, wenn "Cabin" gegeben ist.
Analyse
Frauen mit Pclass=3
Hier gibt es der Grund, warum ich mit meinem Ergebnis nicht zufrieden bin.
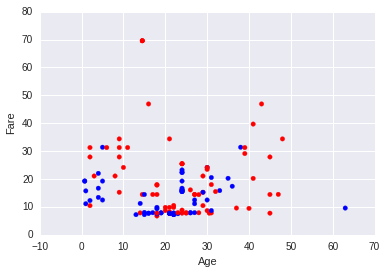
Die blauen Punkte sind die Frauen, die überlebt haben.
Es scheint mir, als ob es keine einfache Regel geben würde. Deshalb habe ich versucht, ein gutes Vorhersagemodell mit maschinellem Lernen zu erstellen. Die geschätzten Genauigkeiten sind:
- GKP-Modell (ohne maschinelles Lernen) : 0.5833
- Random Forest (mit 'Fare', 'Age', 'Parch', 'SibSp'): 0.6736
- Logistische Regression (mit 'Fare', 'Age', Grenze=0.624): 0.7133
- SVM (mit 'Fare', 'Age', 'Parch', 'SibSp'): 0.7152
Deshalb habe ich gedacht, dass ich die Prognose mit SVM oder logistische Regression sehr gut verbessern kann. Aber die richtigen Genauigkeiten von dem maschinellen Lernen ist sogar schlechter als die Genauigkeit von dem GKP-Modell! Deswegen habe ich mich entscheidet, kein maschinelles Lernen zu verwenden.
Männer mit Pclass=1 und inCabin=1
Das GKP-Modell sagt, dass keine Männer überlebt haben. Deshalb kann ich das Modell verbessern, wenn ich einen Teil von überlebten Männern finde.
| inCabin | Survived | CountInTrain | CountInTest | NaiveCount |
| 0 | 0.222222 | 27 | 17 | 13 |
| 1 | 0.410526 | 95 | 40 | 23 |
Das folgende Diagramm zeigt die Männer mit Pclass = 1 und inCabin = 1.
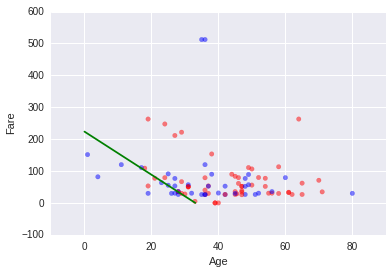
Natürlich habe ich zuerst maschinelles Lernen versucht. Die geschätzten Genauigkeiten sind:
- GKP-Modell: 0.5895
- SVM (mit 'Fare', 'Age', 'FamilySize') 0.589473684211
- Random Forest (mit 'Fare', 'Age', 'Parch', 'SibSp') : 0.610526315789
SVM und Random Forest könnten keinen großen Unterschied machen.
Aber man kann vielleicht finden, dass es überlebte Männer im Diagramm unten links gibt. Deshalb habe ich versucht, eine Entscheidungsgrenze wie die grüne Linie im Diagramm zu finden. Dafür habe ich die Männer gelöscht, die mehr als $500 für das Ticket ausgegeben haben, weil ich die Männer als "outlier" beobachtet habe. Danach habe ich logistische Regression verwendet. Die geschätzte Genauigkeit davon ist 0.675 mit der Grenze 0.471. Darüber hinaus erfolgt das Modell, die Genauigkeit für die Test-Daten zu verbessern.
Männer mit Pclass=2 und inCabin=0
| inCabin | Survived | CountInTrain | CountInTest | NaiveCount |
| 0 | 0.127451 | 102 | 59 | 51 |
| 1 | 0.666667 | 6 | 4 | 2 |
Ich habe die Männer mit Pclass=2 und inCabin=0 ignoriert, weil nur wenig Männer zu der Gruppe gehören.
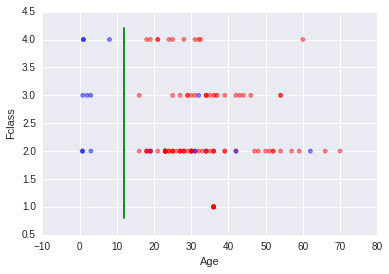
Aus der Grafik wird deutlich, dass viele Junge überlebt haben. Deshalb habe ich die Entscheidungsgrenze Age=14 gestellt.
Ich habe für diese Gruppe kein maschinelles Lernen verwendet. Die Genauigkeit von dem Geschlechte-Modell ist 0.87 für die Gruppe. Ich zweifle, dass man ein besseres Vorhersagemodell mit maschinellem Lernen erstellen kann.
Aber am wichtigsten ist, dass die Entscheidungsgrenze auch für die Test-Daten keine Rolle spielt. Schade.
Männer mit Pclass=3 und FamilySize ≥ 3
Für Männer mit Pclass=3 spielt "FamilySize" eine Rolle. Die folgende Grafik zeigt die Männer mit Pclass=3 und FamilySize ≤ 3.
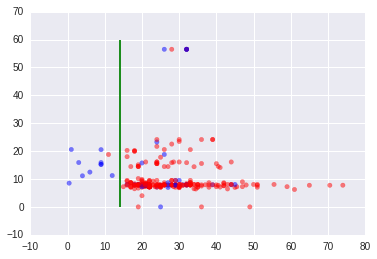
Und die folgende Grafik zeigt die Männer mit Pclass=3 und FamilySize ≥ 4. Die grünen Linien sind "Age=14".
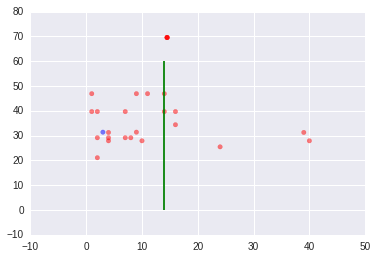
Ich habe maschinelles Lernen versucht, aber es war nicht erfolgreich. Die Genauigkeit von dem GKP-Modell ist schon 0.8645 für die Gruppe von den Männern mit Pclass=3. Ich denke, dass es schwierig ist, ein besseres Vorhersagemodell mit maschinellem Lernen zu erstellen.
Das Ergebnis
Mein Vorhersagemodell
- Frauen
- Pclass=3 & Fclass ≥ 3 ⇒ nicht überlebt
- sonst ⇒ überlebt
- Männer
- Pclass=1 & inCabin=1 ⇒ Logistische Regression
- Pclass=3 & inCabin=0 & FamilySize ≥ 3 & Age ≥ 14 ⇒ überlebt
- sonst ⇒ nicht überlebt.
Mit diesem Vorhersagemodell bekomme ich 0.78947.
Mein Eindruck
Durch die Aufgabe kann man verstehen, wie maschinelles Lernen nicht funktioniert. Das GKP-Modell beschreibt schon sehr gut die Daten. In diesem Fall ist es schwierig, dass maschinelles Lernen gut das Vorhersagemodell verbessert. Aber ich bin noch nicht damit einverstanden, mit maschinellem Lernen die Genauigkeit der Gruppe von Frauen mit Pclass=3 nicht verbessern zu können. Weil der Punkt auf 25% der Test-Daten bestimmt wird, glaube ich noch, dass SVM auf den ganzen Daten gut machen kann.

